ジャンケンで決着がつくまでの回数（6）

平均と分散を求めたので、
今度は正確な分布を求めよう。

n人でm回かかる確率をp(n,m)とすると、
1回で1人になる場合、2人になる場合、…をたし合わせて、

p(n,m) = P(n,1)p(1,m-1) + ... + P(n,n)p(n,m-1) (m > 1)
p(n,1) = P(n,1)

ここで、P(k,l)はk人から1回でl人になる確率で、

P(k,l) = _kC_l / 3^k (l < k)
P(k,k) = 1 - P(k,1) - ... - P(k,k-1) = (2^k - 2) / 3^k

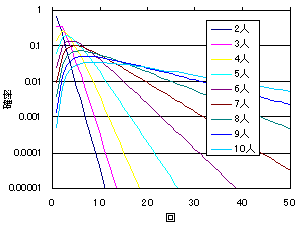
これを計算すると次のようになった。

直線になっているということは、
指数関数的になっているということ。

ソースは次のよう。

var p = [ ];

var P = [ ];

P[1] = [ ];

P[1][0] = 1;
for(var n = 2; n <= 10; n++) {

    P[n] = [ ];

    P[n][0] = P[n-1][0] / 3;

    P[n][n] = 1;

    for(var k = 1; k < n; k++) {

        P[n][k] = P[n][k-1] * (n - k + 1) / k;

        P[n][n] -= P[n][k];

    }

    

    p[n] = [ 0, P[n][1] ];

    for(var i = 2; i <= 50; i++) {

        p[n][i] = 0;

        for(var k = 2; k <= n; k++)

            p[n][i] += P[n][k] * p[k][i-1];

    }

    

    print(p[n]);

}
function print(str) {

    WScript.Echo(str);

}