zzの逆関数（2） - inamori’s diary

まず、z^z = 1 の解を考える。

$z \equiv x + iy \equiv e^{s + it} \equiv e^u$

とする（x, y, s, tは実数）。

$z^z = e^{ue^u} = 1$

より、

$ue^u = 2\pi ni$

nは整数。
nが0なら、uが0で、zは1となる。
nは正とする。負なら共役複素数を考えればよい。

再び、

$u \equiv e^{v + iw}$

とおくと（v, wは実数）、

$e^{v + s + i(w + t)} = 2\pi ni$
$s = e^v\cos{w}$
$t = e^v\sin{w}$
$v + e^v\cos{w} = log(2\pi n)$
$w + e^v\sin{w} = \frac{\pi}{2}$

最後は多価だが、これだけ考えればよい。
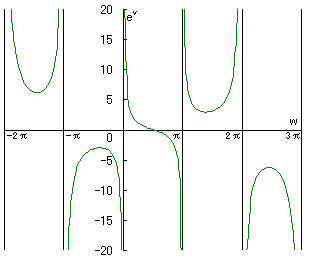
これから、

$e^v = \frac{\frac{\pi}{2} - w}{\sin{w}}$

これのグラフは、

もっとも、e^vが0以下になるところは意味なし。
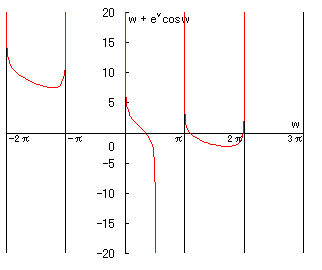
また、v + e^vcos w を w の関数と考えてグラフを書くと、

これが、log(2πn)となるvは無数にあることがわかる。
すなわち、解はバラバラに加算個ある。