ラマヌジャンの高度合成数

英語ではHighly composite numberです。これより小さい数は全て、約数の個数が自分のそれより小さい自然数です。なぜこれが重要なのかは知りません。

これはProblem 110のコードを少し改変するだけで得られます。1分以内に約数の個数が10¹²以内の高度合成数な数を求められました。1を含めると750個です。

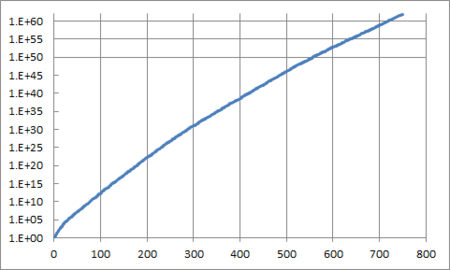
グラフを書いてみましょう。まずは、何番目の高度合成数がどれくらいの大きさか見ます。

k番目の高度合成数をHCN(k)と書くと、

HCN(n) 〜 Ce^{n^0.8}

くらいになるようです。ここから0.8よりは小さくなるようですが。
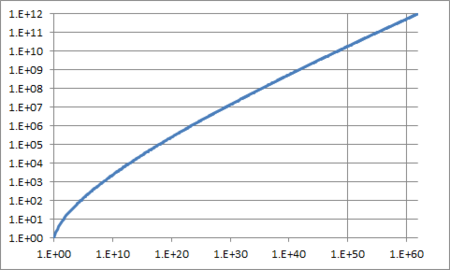
もう一つ、高度合成数と約数の個数を見てみます。

nの約数の個数をd(n)と書くと、

d(n) 〜 Ce^{n^0.7}

くらいになるようです。

from itertools import *
from Queue import PriorityQueue
from math import log
import sys
import time

def gen_sorted(init, nexts):
    pq = PriorityQueue()
    pq.put(init)
    while not pq.empty():
        e = pq.get()
        yield e
        for e1 in nexts(e):
            pq.put(e1)

def is_prime(n):
    return all(n % p != 0 for p in xrange(2, n))

def gen_primes(M):
    for p in (n for n in count(2) if is_prime(n)):
        yield p
        if M == 0:
            break
        M /= 2

def gen_possible_to_add(es):
    yield 0
    e0 = es[0]
    for k in xrange(1, len(es)):
        if es[k] < e0 - 1:
            break
        yield k

def is_possible_to_add(es):
    # e + 3 <= 3 * (e + 1 - q)
    # 2e >= 3q
    p_next = primes[len(es)]
    return any(es[k] * 2 < 3 * qs[len(es)][k]
                    for k in gen_possible_to_add(es))

def nexts((n, es, m)):
    e0 = es[0]
    if e0 == 1:
        es1 = es + (1,)
        yield (n * primes[len(es)], es1, m * 2)
    else:
        if not is_possible_to_add(es):
            return
        for k in xrange(1, len(es)):
            if es[k] == e0 - 1:
                es1 = es[:k] + es[:1] + es[k+1:]
                yield (n * primes[k], es1, m / e0 * (e0 + 1))
                break
            elif es[k] < e0 - 1:
                break
    
    es2 = (e0 + 1,) + es[1:]
    yield (n * 2, es2, m / (e0 + 1) * (e0 + 2))

t0 = time.clock()
E = 12
N = 10 ** E
primes = list(gen_primes(N))
L = len(primes)
qs = [ [ int(log(primes[l]) / log(primes[k]) + 1) for k in xrange(L) ]
                                                    for l in xrange(L) ]
prev_m = 1
for n, es, m in takewhile(lambda x: x[2] < N, gen_sorted((2, (1,), 2), nexts)):
    if m > prev_m:
        print n, m
        prev_m = m
print >>sys.stderr, time.clock() - t0